求解方程式
本文专门介绍用Excel求解方程式的方法。
一、求解超越方程
不能用系数表达根的方程式称为超越方程。求解超越方程通常有两种方法,一种是图解法,一种是迭代法。这两种方法,手工计算都十分麻烦,利用Excel可以迅速获得结果。
我们用
1、图解法
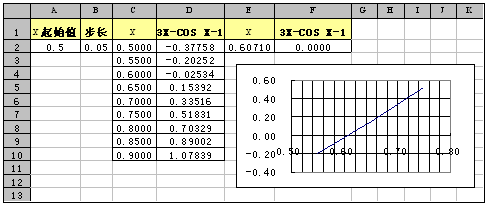
在A2单元格设定X的起始值(单位为弧度),在B2单元格设定X的步长(X每步的增加值)。在C2单元格输入公式“= A2”,在C3单元格输入公式“= C2+$B$2”(带$表示B2单元格为绝对地址,复制公式时地址不发生变化),点住C3单元格右下角向下拖若干行,复制公式,完成各步的X值设置。在D2单元格输入方程式公式“=3*C2-COS(C2)-1”, 点住D2单元格右下角向下拖动,复制公式,完成方程式各步的计算工作。分析D列的计算结果,目的是寻找当方程式值为0时,X的变化区间。如果D列的数值不在0附近,可调整A2(X的起始值);如果D列数值变化过大,可减小 B2(X的增步长),直到满意为止。调整A2和B2时,其它数值会自动变化。
以D列0 为中心,选取上下附近C、D两列的相应区域,点“插入”菜单的“图表”,选区“XY散点图”,按照“图表向导”一步一步的做下去,调整好坐标轴的起止数值,增加X轴的“次要网格线”,以达到方程式曲线在穿越X轴(方程式值为0)时,能清晰辨认X的数值。从图上可以看到,方程式曲线穿越X轴的数值约为6.07,这就是超越方程的解。图解法求解超越方程,其优点是可以观察方程式的变化趋势,以及X值对方程式的影响情况,缺点是精度较低。
2、迭代法
用迭法求解一元方程的利器就是Excel的“单变量求解”工具。计算时需要将求解的公式输入到某个单元格作为“目标单元格”。本例只需点D2单元格,点“复制”,再点F2单元格,点“粘贴”,即可将公式复制到F2单元格,这样,F2就是“目标单元格”,E2自然成为X的变量单元格。
点F2单元格,点“工具”菜单的“单变量求解”。设“目标单元格”为F2,设“目标值”为0,设“可变单元格”为E2,点“确定”,即得计算结果:X=0.6071。
用“单变量求解”求解一元方程,优点是迅速、准确,缺点是不能了解函数的变化过程。
二、求解联立方程
用Excel求解联立方程有两个方法,一个是使用矩阵函数,一个是使用“规划求解”工具,两个方法都十分简便。
以下列3元联立方程为例说明求解方法。

1、矩阵法
联立方程一般可以用矩阵表示为AX=B,由此X=A-1B。式中:A-1为系数矩阵的逆矩阵,B为联立方程右侧的常量矩阵,取两矩阵的积,即得联立方程的解。
在A2:C4区域设置系数矩阵A,在D2:D4设置常数矩阵B。选取F2:F4,输入公式“=MMULT(MINVERSE(A2:C4),D2:D4)”,同时按Shift 键、Ctrl键和 Enter键,即得计算结果:X1=2、X2=3、X3=-2.5。
说明1,MMULT为矩阵积函数,用来计算矩阵的乘积。MINVERSE为逆矩阵函数,用来计算逆矩阵。这里将两个函数组合使用,可以减少计算步骤。
说明2,当在Excel上进行成组计算时,称为数组操作。数组的计算必须同时按Shift 键、Ctrl键和 Enter键,方才有效。数组操作的同时,将自动在公式两侧产生大括符,表示该运算为数组运算。
2、规划求解
规划求解是Excel的特殊工具,主要用于系统规划中的最优化问题,拿来求解常规的联立方程,自然游刃有余。
设H2:H4为X1、X2、X3的变量区,在I2输入公式“=2*H2-2*H3+4*H4”,在I3输入公式“=2*H2+3*H3+2*H4”,在I4输入公式“=-H2+H3-H4”。在I5输入公式“=SUM(I2:I4)”,计算联立方程常数项的和,其值为-12+8+3.5=-0.5,I5可设置成目标单元格,-0.5就是目标值。点I5,点“工具”菜单的“规划求解”。“目标单元格”设为I5,“目标值”设为-0.5,“可变单元格”设为H2:H4。点“添加”,设置以下“约束”:I2=-12、I3=8、I4=3.5。点“求解”,完成计算,即得计算结果:X1=2、X2=3、X3=-2.5。

三、求解有约束的方程
所谓有约束的方程,就是除了主要方程式(称作目标函数)外,还带有若干附加条件。目标函数和这些附加条件未必都是“等于”的关系,它们可以是“大于”,可以是“小于”,也可以是“最大”或“最小”,方程式的数量也未必和未知变量相等,求解这类方程,显然不是一般代数方法能够奏效的。计算有约束方程的方法,在运筹学中称为“最优化问题”,Excel为此设计了“规划求解”专用工具。“规划求解”可以解决社会、经济、工程诸多实际问题,这里我们只用一个数值例子,说明具体计算方法。
今有目标函数 ![]() ,要求在以下约束下,获得最大值。
,要求在以下约束下,获得最大值。
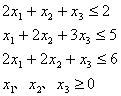
这是一个求最大值的问题,方程式(不等式)的数量也超过变量的数目,所以只能用“规划求解”方法计算。
我们在Excel表格中,设A2、B2、C2分别为X1、X2、X3三个变量(计算前为空格),在D2单元格输入目标函数公式“=3*A2+B2+3*C2”, 在E2单元格输入第一约束条件“=3*A2+B2+C2”, 在F2单元格输入第二约束条件“=A2+2*B2+3*C2”, 在G2单元格输入第三约束条件“=2*A2+2*B2+C2”。
点“工具”菜单的“规划求解”, “目标单元格”设为D2,“目标值”设为“最大值”,“可变单元格”设为A2:C2。点“添加”,设置以下约束:E2≤2、F2≤5、G2≤6、A2:C2≥0。点“求解”,稍等片刻即得计算结果:X1=0.2、X2=0、X3=1.6,在此条件下,目标函数的最大值为5.4。
 按Shift 键、Ctrl键和 Enter键,即得计算结果:X1=2、X2=3、X3=-2.5。
按Shift 键、Ctrl键和 Enter键,即得计算结果:X1=2、X2=3、X3=-2.5。
说明1,MMULT为矩阵积函数,用来计算矩阵的乘积。MINVERSE为逆矩阵函数,用来计算逆矩阵。这里将两个函数组合使用,可以减少计算步骤。
说明2,当在Excel上进行成组计算时,称为数组操作。数组的计算必须同时按Shift 键、Ctrl键和 Enter键,方才有效。数组操作的同时,将自动在公式两侧产生大括符,表示该运算为数组运算。
2、规划求解
规划求解是Excel的特殊工具,主要用于系统规划中的最优化问题,拿来求解常规的联立方程,自然游刃有余。
设H2:H4为X1、X2、X3的变量区,在I2输入公式“=2*H2-2*H3+4*H4”,在I3输入公式“=2*H2+3*H3+2*H4”,在I4输入公式“=-H2+H3-H4”。在I5输入公式“=SUM(I2:I4)”,计算联立方程常数项的和,其值为-12+8+3.5=-0.5,I5可设置成目标单元格,-0.5就是目标值。点I5,点“工具”菜单的“规划求解”。“目标单元格”设为I5,“目标值”设为-0.5,“可变单元格”设为H2:H4。点“添加”,设置以下“约束”:I2=-12、I3=8、I4=3.5。点“求解”,完成计算,即得计算结果:X1=2、X2=3、X3=-2.5。

三、求解有约束的方程
所谓有约束的方程,就是除了主要方程式(称作目标函数)外,还带有若干附加条件。目标函数和这些附加条件未必都是“等于”的关系,它们可以是“大于”,可以是“小于”,也可以是“最大”或“最小”,方程式的数量也未必和未知变量相等,求解这类方程,显然不是一般代数方法能够奏效的。计算有约束方程的方法,在运筹学中称为“最优化问题”,Excel为此设计了“规划求解”专用工具。“规划求解”可以解决社会、经济、工程诸多实际问题,这里我们只用一个数值例子,说明具体计算方法。
今有目标函数 ![]() ,要求在以下约束下,获得最大值。
,要求在以下约束下,获得最大值。
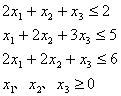
这是一个求最大值的问题,方程式(不等式)的数量也超过变量的数目,所以只能用“规划求解”方法计算。
我们在Excel表格中,设A2、B2、C2分别为X1、X2、X3三个变量(计算前为空格),在D2单元格输入目标函数公式“=3*A2+B2+3*C2”, 在E2单元格输入第一约束条件“=3*A2+B2+C2”, 在F2单元格输入第二约束条件“=A2+2*B2+3*C2”, 在G2单元格输入第三约束条件“=2*A2+2*B2+C2”。
点“工具”菜单的“规划求解”, “目标单元格”设为D2,“目标值”设为“最大值”,“可变单元格”设为A2:C2。点“添加”,设置以下约束:E2≤2、F2≤5、G2≤6、A2:C2
(责任编辑:admin)




