Excel2000 应用案例之三十五
时间：2005-02-18 11:55 来源：Excel Home 作者：admin 阅读：次
②建立回归模型
通常，在相关分析的基础上必须拟合回归模型，以便进行推算、预测。建立回归模型的具体操作步骤如下：选择工具菜单中的数据分析命令，弹出数据分析对话框。
在分析工具列表框中，选回归工具。
这时，将弹出回归对话框，如图8－9所示。
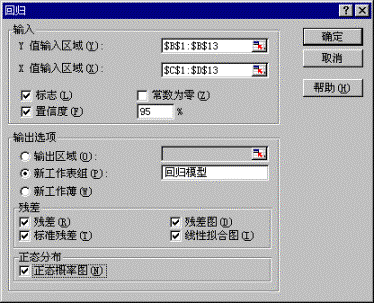
图8－9
指定输入参数。在输入Y区域、输入X区域指定相应数据所在的单元格区域，本例分别指定为B1:B13和C1:D13，并选定标志复选框，在置信水平框内键入95%。对于一些特殊的回归模型，可以根据需要指定常数为0（即
）。 指定输出选项。这里选择输出到新工作表组，并指定工作表名称为“回归模型”，选定残差（即随机误差项）和正态分布中的所有输出选项，以观察相应的结果。
单击确定按钮。
最后得到回归分析的计算结果。图8－10是有关回归分析的统计量、方差分析表和回归系数及其
检验、预测区间等数据；图8－11给出了预测值、残差值以及所计算的DW统计值；图8－12给出了自变量 
（科研人员）与 
（科研经费）的残差分析图；图8－13给出了自变量 
与 
的最佳适配回归线图；图8－14给出了样本百分比排位及正态概率图。 分析图8－10、8－11中的计算结果，可得下述检验结论（本例样本个数n=12，解释变量个数k=2）。
检验：在回归统计区域A3:B8中，给出的 
为0.997644，调整后的 
为0.997121，均很接近1，说明 
与 
的关系很密切。 
检验：在方差分析区域A10:F14中，给出的 
检验值为1905.786远远大于 
=4.26，说明 
与 
之间的回归效果非常显著。 
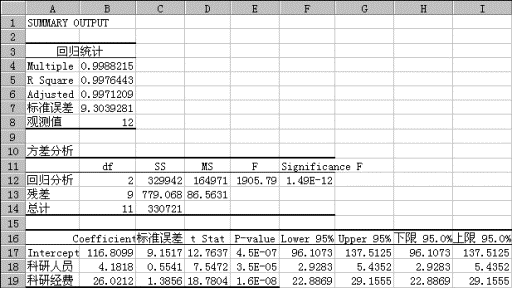
图8－10
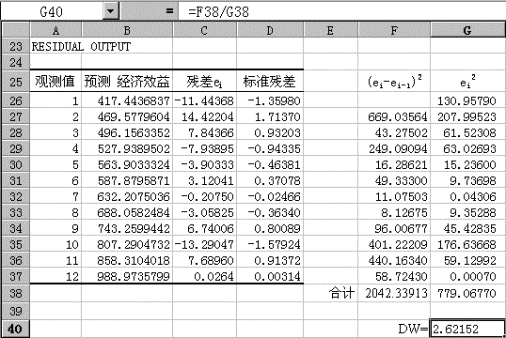
图8－11
检验：在回归模型区域A16:I19中，给出了回归系数 
的估计值及其标准误差、 检验值和回归系数估计区间的上下限等。由于各回归系数的 
检验值分别为 
=12.7637， 
=7.5472， =18.7804，都大于 
=2.2622，故拒绝原假设 
=0， 
=0和 
=0。即可以断言：科研人员与科研经费对该企业的经济效益有显著影响。 
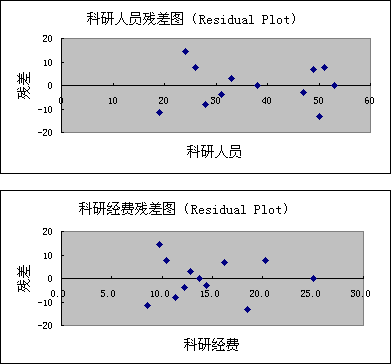
图8－12
图8－13
图8－14
DW检验：在Excel给出的回归分析结果中没有给出DW检验值。因此，需要自行按公式计算DW统计值。方法是：先利用公式分别求出
之值，再单击工具栏上的求和按钮计算 
，最后将两个求和值相除便可求的DW值。如图8－11中的G40单元格所示。对于给定的显著性水平为 
=0.05，解释变量个数 
=3、样本个数 
=12，查DW检验表。因DW检验表中样本容量 
最小为15，故取临界值 
=0.82， 
=1.75，于是有DW统计值在 
=0.82＜DW=2.62152＜4－ 
=2.25之间。所以该回归模型不存在自相关，通过计量经济检验。 综合上述计算结果和检验结果，可得如下的回归模型：
这是一个较为优良的回归模型。现在利用该回归模型，就可以根据预测期的科研人员与科研经费，对该企业未来的经济效益进行预测。
现假定1999年该企业科研人员61名、科研经费40万元，即预测期的解释变量矩阵为
，则1999年该企业的经济效益的预测值为： 
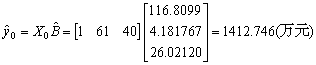
因标准误差S=9.3039281，样本个数n=12，解释变量个数k=2，则在显著性水平
=0.05下，1999年该企业的经济效益的预测区间为： 
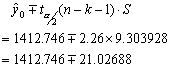
即：当1999年该企业的科研人员61名、科研经费40万元时，在α=0.05显著性水平下，该企业1999年的经济效益预测区间在1391.719～1433.773万元之间。
(责任编辑：admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容