Excel2000 应用案例之二十五
时间：2005-02-18 11:47 来源：Excel Home 作者：admin 阅读：次
6.2.3 样本率差异检验
当需要进行检验的数据是计数资料时，通常需要采用Χ2检验（Chi-quare test）。它可用来检验两个或是多个样本率之间差异的显著性；两个数列之间差异的显著性，或是两种属性、特征之间是否具有依存关系等。例如，某医院对300名鼻咽癌患者和499名健康人的血型进行了检查，所得资料如下所示，现需要分析鼻咽癌患者与健康人的血型组成有无显著差异？
|
组别 |
A |
B |
O |
AB |
|
鼻咽癌组 |
64 |
86 |
130 |
20 |
|
健康组 |
125 |
138 |
210 |
26 |
1. 样本率差异检验的基本理论
Χ2检验主要是检验观察的实际数与假设的理论数符合的程度。也就是说，原假设
认为理论上的结论与实际情况相符合。Χ2检验所需的统计量是服从Χ2分布的统计量。对于实际问题，其计算过程是先根据下述公式计算出理论数：
式中TRC为第R行第C列的理论数，NR为与理论数同行的实际数的合计数，NC为与理论数同列的实际数的合计数，N为实际数的总计。所以理论数实际上是依据检验的两组数据无显著差异的假设推算的平均值。上述问题的理论数计算结果如下：
|
组别 |
A |
B |
O |
AB |
|
鼻咽癌组 |
64 |
86 |
130 |
20 |
|
健康组 |
125 |
138 |
210 |
26 |
式中A为实际数，T为理论数，由于同一行内
的代数和为0，所以采用 
计算。计算该值与T的比值，在于观察 
所占比重的大小。 
的总和即为Χ2值，反映了实际数与理论数相差的情况。检验拒绝域为：对于给定的显著性水平
，当 
时拒绝原假设 
，此时认为实际数与理论数的差别较大，即认为检验的数据之间存在显著的差异。其中 
的自由度n等于样本数据的行数减1与列数减1的乘积。2. 样本率差异检验的操作
Excel 2000没有直接提供Χ2检验的数据分析工具，所以要进行有关样本率差异的检验，需使用有关的函数进行。而且相应的函数不自动计算理论数，需要手工计算，因此操作步骤相对较为繁琐。
首先将有关原始数据输入到工作表中。并计算出各行、列的合计。
在工作表的另一个单元格区域中计算出对应的理论数。在计算公式中要注意相对地址和混合地址的正确使用。本例是在B8单元格输入公式：“=$F3*B$5/$F$5”，然后将其填充到B9以及C8:E9单元格区域。如图6－12所示。
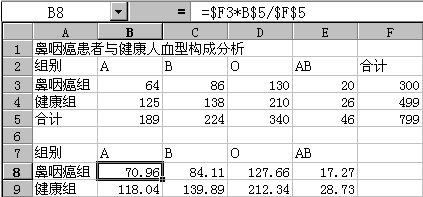
图6－12
在G8单元格输入利用CHITEST函数计算Χ2统计概率的公式。该函数有两个参数，分别为观察值所在的单元格区域和理论值所在的单元格区域，分别是B3:E4和B8:E9。如图6－13所示。
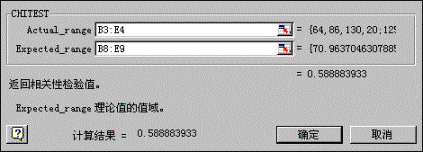
图6－13
在G9单元格输入利用CHIINV函数计算Χ2的公式。该函数有两个参数，分别为Χ2的概率和自由度。其中前者为CHITEST函数计算的结果，后者等于样本数据的行数减1与列数减1的乘积为3。如图6－14所示。
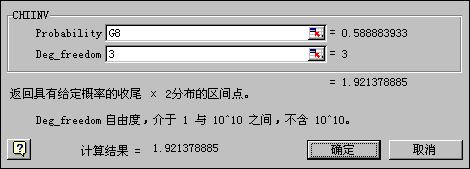
图6－14
根据计算结果判断是否接受原假设。因为 
=7.81＞1.92（本例计算结果见图6－14），所以在显著性水平0.05下，接受原假设，即认为鼻咽癌患者与一般健康人的血型组成无显著差异。
(责任编辑：admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容