Excel2000 应用案例之三十二
时间：2005-02-18 11:52 来源：Excel Home 作者：admin 阅读：次
8.2 回归分析预测法
在实际经济问题中，某一经济行为常受多因素的影响和制约。例如，商品的销售量与商品的价格、商品的质量以及消费者的收入水平等因素有关；又如果树的产量受施肥量、降雨量、气温等因素的影响。因此，要研究该经济行为就应从事物变化的因果关系出发，寻找它与其他因素之间的的内在联系，这就是因果关系分析法。在因果关系分析法中最常用的方法之一就是回归分析法。回归分析预测法就是从各种经济现象之间的相互关系出发，通过对与预测对象有联系的现象变动趋势的分析，推算预测对象未来状态数量表现的一种预测方法。
根据回归分析中所考虑因素的多少，可将回归分析分为一元回归分析和多元回归分析。例如，对于耐用消费品销售量与居民收入的相关关系的分析问题就属于一元回归分析；而对于粮食产量与施肥量、降雨量、气温的相关关系的分析问题就属于多元回归分析。一元回归分析实质上多元回归分析的一种特例。
根据回归模型是否是线性的，又可将回归分析分为线性回归分析和非线性回归分析。例如，若耐用消费品销售量与居民收入具有线性关系，则属于线性回归分析问题；若某商店的商品流通费用率与销售额具有曲线关系，则属于非线性回归分析问题。
本节先讨论多元线性回归法，然后再讨论非线性回归问题。
8.2.1 线性回归预测法
1. 多元线性回归模型
设所研究的对象
受多个因素 
的影响，假定各个影响因素与 
的关系是线性的，则可建立多元线性回归模型： 
式中
代表影响因素，通常是可以控制或预先给定的，故称为解释变量或自变量； 
代表各种随机因素对 
的影响的总和，称为随机误差项，根据中心极限定理，可以认为它服从正态分布，即 
； 
就是所研究的对象，即预测目标，称为被解释变量或因变量。 根据n组观测值
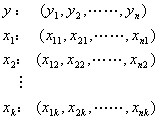
则有
写成矩阵形式
其中
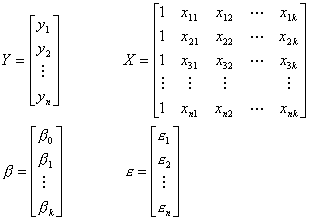
利用最小二乘法可得回归系数向量
的估计值 
为 
故回归分析模型为
(责任编辑：admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容