Excel2000 应用案例之三十三
时间：2005-02-18 11:53 来源：Excel Home 作者：admin 阅读：次
2. 多元线性回归模型的检验求出的回归模型是否合理，是否符合变量之间的客观规律性，引入所影响因素是否有效，变量之间是否存在线性相关关系，模型能否付诸应用，这要通过检验决定。一般讲，回归模型必须通过三方面的检验：经济意义检验、统计检验和计量经济学检验。只有当所有检验都通过时，所做的回归模型才成立。才能利用连贯性、相关性和类推性原则，根据过去和现在的规律预测未来。当然，还应从经济角度上分析模型的预测值是否合理？是否符合经济规律？是否可行等等？①经济意义检验首先需要检验模型是否符合经济意义，检验求得的参数估计值的符号与大小是否合理，是否与根据人们的经验和经济理论所拟定的期望值相符合。如果不符，则要查找原因和采取必要的修正措施，重新建立模型。②统计检验统计检验是运用数理统计的方法，对方程进行检验、对模型参数估计值的可靠性进行检验。这主要包括拟合优度检验、方程显著性检验、变量显著性检验，即常用的 检验、F检验和  检验。 拟合优度检验（  检验）：检验所有解释变量与被解释变量之间的相关程度 拟合优度检验就是检验回归方程对样本观测值的拟合程度。常用的方法是  检验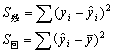，又称为复相关系数检验法，它是通过对总变差（总离差）  的分解得到。  其中  总变差平方和  是各个观察值与样本均值之差的平方和，反映了全部数据之间的差异；残差平方和  是总变差平方和中未被回归方程解释的部分，由解释变量  中未包含的一切因素对被解释变量  的影响而造成的；回归平方和  是总变差平方和中由回归方程解释的部分。 显然，对于一个好的回归模型，它应该较好地拟合样本观测值，  中  越小越好。于是可以用：  对回归方程的拟合优度进行检验。如果所有样本观测值都位于回归方程上，即：  此时回归方程完全拟合了样本观测值，  等于1。当然，完全拟合的情况是不可能的，  不可能等于1，但毫无疑问，  越接近1，回归方程的拟合优度越高。 通常，  称为复可决系数，取值范围为0≤  ≤1，其平方根  称为复相关系数（当解释变量的个数为1时，  称为相关系数）。这里，  说明了在被解释变量  的总变差中，由一组解释变量  的变动所引起的百分比；  则描述了一组解释变量  与被解释变量  之间的线性相关程度。例如  =0.93，可以说  值的变化有93%因  的变化而产生。因此，若 的值愈接近1，则表示  与  的关系愈密切。 由于  是一个随解释变量个数的增加而递增的增函数，所以为使拟合优度检验指标不仅能反映已被解释的变差与总变差的关系，而且能反映回归模型中所包含的解释变量个数的影响，需要调整  ，记为  。  式中  为残差平方和  的自由度，  为总变差平方和  的自由度。根据  与  的定义式可推导出两者的关系式为：  从上式可以看出：当  时，  ＜  ，这说明  中包含了解释变量个数的影响，随着解释变量个数的增加，  总是小于  ；尽管  总是非负的，但  却可能为负，若遇到  为负数的情况，  取值为零。 在实际应用中，  到底多大时回归模型才算通过了拟合优度检验呢？这并无绝对标准，要根据具体情况而定，因为拟合优度并不是检验回归模型的唯一标准，有时为了使模型有较合理的经济解释，可能会在某种程度上牺牲拟合优度。这就是说模型的合理的经济解释是第一位的。 方程显著性检验（  检验）：判断被解释变量与所有解释变量之间是否线性关系 对于多元线性回归方程，方程显著性检验就是对总体的线性关系是否显著成立作出推断，即检验被解释变量  与所有解释变量  之间的线性关系是否显著，这就要检验假设：   ：至少有一个  不为零 应用数理统计理论可以证明：  与  相互独立，且当  为真时，  与  分别服从自由度为  的  分布，故有：  即  统计量服从以（  ）为自由度的  分布。 首先根据样本观测值及回归值计算出统计量  ，于是在给定的显著性水平  下，若  ，则拒绝  ，判定被解释变量  与所有解释变量  之间的回归效果显著，即确实存在线性关系；反之，则不显著。 比较  统计量与  检验值可以看出，在  一定时，  大，即拟合优度高，  统计量的值也大，容易通过方程显著性检验，拟合优度检验与方程显著性检验是一致的，只是前者比较模糊，后者更加定量化。一般来说，当拟合优度  ＞0.80时，相应的  统计量的值将达到两位数，只要样本容量  适当，通过方程显著性检验是没有问题的。 变量显著性检验（  检验）：挑选重要因素，剔除可有可无的因素 前面讲的  检验和  检验都是将所有的解释变量作为一个整体来检验它们与被解释变量  的相关程度以及回归效果，但对于多元回归模型，方程的显著性并不意味每个解释变量对被解释变量  的影响都是重要的。如果某个解释变量并不重要，则应该从方程中把它剔除，重新建立更为简单的方程。所以必须对每个解释变量进行显著性检验。这等价于对每个解释变量检验假设   其中  。 应用数理统计理论可以证明：当 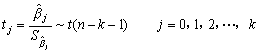 为真时，统计量  服从自由度为  的  分布，即：  在给定的显著性水平  下，若  ，则拒绝  ，说明解释变量  对被解释变量  有显著影响，即  是影响  的主要因素；反之，接受  ，说明解释变量  对被解释变量  无显著影响，则应删除该因素。 需要说明的是，当影响  的主要因素只有一个变量  时，问题变成了一元回归分析，此时  检验和  检验的作用是一样的，因此可以不用再做  检验了。 ③计量经济学检验在回归分析法中，假设随机误差项在不同的样本点之间是不相关的，即 与  （  ）相互独立。但在实际问题中，经常出现与此相违背的情况，  与  （  ）之间存在相关性，称为序列相关。若存在序列相关，则此时的回归模型无效，必须重新建立回归模型。 在序列相关中，最常见的是  与  相关，称为一阶自相关。最常用的检验方法是DW检验法，定义DW统计量为：  其中：  ，是  的估计值。 分析可知：当  与  正自相关时，DW≈0；当  与  负自相关时，DW≈4；当  与  不存在自相关或相关程度很小时，DW≈2；可见，DW的取值范围为0~4之间。 在实际应用中，对于给定的显著性水平  以及解释变量个数  、样本个数  ，从DW检验表中查得相应的临界值  和  ，然后利用下表判别检验结论。 DW值 |
检验结果
| 4－ |
 ＜DW＜4 否定假设，存在负自相关 | 0＜DW＜ |
 否定假设，存在正自相关
|  ＜DW＜4－  接受假设，不存在自相关
|  ＜DW＜  检验无结论（不能确定）
| 4－ |
 ＜DW＜4－  检验无结论（不能确定）
| | |||
需要说明的是，回归分析法既适合于利用历史数据即时间序列数据来研究经济变量之间的定量关系，建立预测模型，进行预测分析；又适合于利用同一时期横断面数据来研究经济变量之间的内在联系，分析经济结构，比较经济发展状态及发展趋势。当所研究的数据是横断面数据时，由于数据是同一时期的（例如由今年全国各地不同产区的粮食产量所组成的数据序列），不存在相关性，因此无须做DW检验。
(责任编辑：admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容