Excel2000 应用案例之四十
时间：2005-02-20 13:22 来源：Excel Home 作者：admin 阅读：次
第九章 规划分析
[本章提要]本章主要通过生产管理和经营决策中的最优配置问题，介绍Excel 2000的规划求解工具的应用。着重说明了规划求解工具的适应范围，求解步骤，结果分析以及限制条件的修改。 在生产管理和经营决策过程中，经常会遇到一些规划问题。例如生产的组织安排，产品的运输调度，作物的合理布局以及原料的恰当搭配等问题，其共同点就是如何合理地利用有限的人力、物力、财力等资源，得到最佳的经济效果，即达到产量最高、利润最大、成本最小、资源消耗最少等目标。这些问题中通常要涉及到众多的关联因素，复杂的数量关系，只凭经验进行简单估算显然是不行的。而线性规划、非线性规划和动态规划等方法正是研究和求解该类问题的有效数学方法。但是这些方法的求解大多十分繁琐复杂，常令人望而却步。而利用Excel 2000的规划求解工具，可以方便快捷地帮助我们得到各种规划问题的最佳解。9.1 规划模型
规划问题可以涉及到众多的生产或经营领域的常见问题。例如生产的组织安排问题：如果要生产若干种不同的产品，每种产品需要在不同的设备上加工，每种产品在不同设备上需要加工的时间不同，每种产品所获得的利润也不同。要求在各种设备生产能力的限制下，如何安排生产可获得最大利润。又如运输的调度问题：如果某种产品的产地和销地有若干个，从各产地到各销地的运费不同。要求在满足各销地的需要量的情况下，如何调度可使得运费最小。再如作物的合理布局问题：不同的作物在不同性质的土壤上单位面积的产量是不同的。要求在现有种植面积和完成种植计划的前提下，如何因地制宜使得总产值最高。还有原料的恰当搭配问题：在食品、化工、冶金等企业，经常需要使用多种原料配置包含一定成份的产品，不同原料的价格不同，所含成份也不同。要求在满足产品成份要求的情况下，如何配方可使产品成本最小。虽然规划问题种类繁多，但是其所要解决的问题可以分成两类：一类是确定了某个任务，研究如何使用最少的人力、物力和财力去完成它；另一类是已经有了一定数量的人力、物力和财力，研究如何使它们获得最大的收益。而从数学角度来看，规划问题都有下述共同特征：
决策变量：每个规划问题都有一组需要求解的未知数（
），称作决策变量。这组决策变量的一组确定值就代表一个具体的规划方案。 约束条件：对于规划问题的决策变量通常都有一定的限制条件，称作约束条件。约束条件可以用与决策变量有关的不等式或等式来表示。
目标：每个问题都有一个明确的目标，如利润最大或成本最小。目标通常可用与决策变量有关的函数表示。
如果约束条件和目标函数都是线性函数，则称作线性规划；否则为非线性规划。如果要求决策变量的值为整数，则称为整数规划。规划求解问题的首要问题是将实际问题数学化、模型化。即将实际问题通过一组决策变量、一组用不等式或等式表示的约束条件以及目标函数来表示。这是求解规划问题的关键。然后即可应用Excel 2000的规划求解工具求解。
例如，某企业要指定下一年度的生产计划。按照合同规定，该企业第一季度到第四季度需分别向客户供货80、60、60和90台。该企业的季度最大生产能力为130台，生产费用为
（元），这里的 
为季度生产的台数。该函数反映出生产规模越大，平均生产费用越低。若生产数量大于交货数量，多余部分可以下季度交货，但企业需支付每台16元的存储费用。所以生产规模过大，超过交货数量太多，将增加存储费用。那么如何安排各季度的产量，才能既满足供货合同，且使得企业的各种费用最小呢？ 该问题是一个典型的非线性规划问题。下面首先将其模型化，即根据实际问题确定决策变量，设置约束条件和目标函数。
该问题的决策变量显然应为第一季、第二季、第三季和第四季的产量。设其分别为
。 该问题的约束条件为：
交货数量的约束：
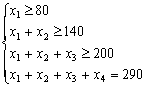
生产能力的约束：
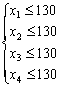
该问题的目标应是企业的费用最小。其中，费用包括生产费用
和可能发生的存储费用 
之和，用公式表示则分别为： 
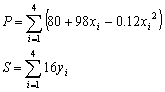
则目标函数
为： 
(责任编辑：admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容