Excel2000 应用案例之三十九
时间:2005-02-20 13:21 来源:Excel Home 作者:admin 阅读:次
例如,某商场1989~1998年的商品流通费用率与商品零售额资料如下表所示。若1999年该商场商品零售额36.33亿元,试预测1999年该商场商品流通费用额。
预测1999年该商场商品流通费用额的具体步骤如下:
根据统计资料绘制出散点图,如图8-17所示。从图中可以看出,随着商品零售额的增加,商品流通费用率有不断下降的趋势,呈现双曲线形状。
建立如下所示的双曲线模型。

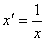
则
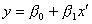
具体实现是:先在D2单元格中输入公式:=1/C2,然后拖拽填充柄将该公式填充到D11 单元格即可。
利用回归工具建立上述回归模型,得如图8-18所示的结果。
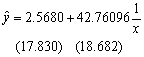
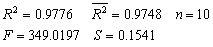
预测。将1999年该商场商品零售额36.33亿元代入模型中,得1999年该商场商品流通费用率为:
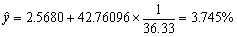
故1999年该商场商品流通费用总额预测值为1.3606万元(36.33×3.74%)。
与线性回归分析类似,非线性回归分析也可以使用函数建立模型。对于非线性回归问题,Excel 2000提供的函数有LOGEST、GROWTH等。有关这些函数的具体使用方法,可通过Excel 2000的函数向导学习掌握。
通过本章内容的学习,应能够针对实际问题,选择有效的预测方法,建立模型,进行预测分析。若分析影响事物的主要因素比较困难或相关变量资料难以得到,则可以采用时间序列预测法(如移动平均法和指数平滑法)。若需要从事物变化的因果关系出发,寻找它与其他因素之间的内在联系,则可以采用回归分析预测法。对于移动平均法、指数平滑法和回归分析预测法,应能熟练地应用Excel 2000的分析工具建立相应模型、进行预测推算。尤其是对于所求出的回归模型,必须通过经济意义检验、统计检验和计量经济学检验。只有当所有检验都通过时,所做的回归模型才成立,才能用于预测。
| 年 份 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 |
| 商品流通费用率 | 7.0 | 6.2 | 5.8 | 5.3 | 5.0 | 4.6 | 4.5 | 4.4 | 4.2 | 4.0 |
| 商品零售额 | 10.2 | 11.7 | 13.0 | 15.0 | 16.5 | 19.0 | 22.0 | 25.0 | 28.5 | 32.0 |
预测1999年该商场商品流通费用额的具体步骤如下:
根据统计资料绘制出散点图,如图8-17所示。从图中可以看出,随着商品零售额的增加,商品流通费用率有不断下降的趋势,呈现双曲线形状。
建立如下所示的双曲线模型。
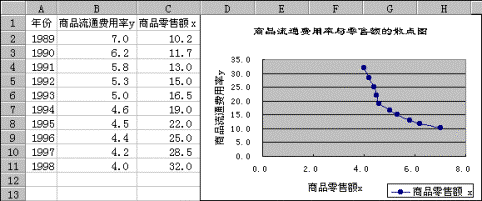
图8-17
先进行倒数变换,令则
具体实现是:先在D2单元格中输入公式:=1/C2,然后拖拽填充柄将该公式填充到D11 单元格即可。
利用回归工具建立上述回归模型,得如图8-18所示的结果。
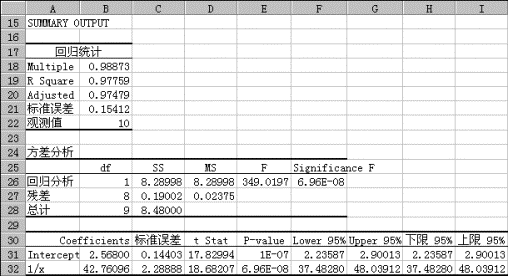
图8-18
分析图8-18中的计算结果,可得如下回归模型: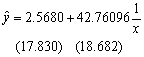
预测。将1999年该商场商品零售额36.33亿元代入模型中,得1999年该商场商品流通费用率为:
故1999年该商场商品流通费用总额预测值为1.3606万元(36.33×3.74%)。
与线性回归分析类似,非线性回归分析也可以使用函数建立模型。对于非线性回归问题,Excel 2000提供的函数有LOGEST、GROWTH等。有关这些函数的具体使用方法,可通过Excel 2000的函数向导学习掌握。
通过本章内容的学习,应能够针对实际问题,选择有效的预测方法,建立模型,进行预测分析。若分析影响事物的主要因素比较困难或相关变量资料难以得到,则可以采用时间序列预测法(如移动平均法和指数平滑法)。若需要从事物变化的因果关系出发,寻找它与其他因素之间的内在联系,则可以采用回归分析预测法。对于移动平均法、指数平滑法和回归分析预测法,应能熟练地应用Excel 2000的分析工具建立相应模型、进行预测推算。尤其是对于所求出的回归模型,必须通过经济意义检验、统计检验和计量经济学检验。只有当所有检验都通过时,所做的回归模型才成立,才能用于预测。
(责任编辑:admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容




