Excel2000 应用案例之二十九
时间:2005-02-18 11:50 来源:Excel Home 作者:admin 阅读:次
2. 基本操作
下面利用Excel 2000提供的方差分析:可重复双因素分析工具求解本例。具体操作步骤如下:
选择工具菜单中的数据分析命令,此时弹出数据分析对话框。
在分析工具列表框中,选方差分析:可重复双因素分析工具。
这时弹出方差分析:可重复的双因素分析对话框,如图7-4所示。

图7-4
在输入框中指定输入参数。在输入区域框中指定试验数据所在区域A1:D9(通常为了使输出结果容易阅读理解,在原始数据区域中应包含标识行和列的标记信息);在每一样本的行数中键入2(因本例的每种原料有两行数据,即对因素A、B的水平的每对组合进行了t=2次试验);在 框内输入显著性水平为0.05。
框内输入显著性水平为0.05。
在输出选项框内指定输出选项。本例选定输出区域,并键入输出区域左上角单元格地址A11。
单击确定按钮。
所得本例的方差分析结果如图7-5所示。

图7-5
在图7-5给出的统计结果中,单元格区域A46:E52中的数据正好与表7-2所示的双因素重复试验方差分析表中的各个统计量相对应,其中样本即为行因素A,列即为列因素B,交互即为因素A与B的交互作用,内部即为误差,总计即为总和,差异源即为方差来源,SS即为平方和,df即为自由度,MS即为均方,F即为F比,P-value为接受原假设 的概率,F crit为拒绝域的临界值
的概率,F crit为拒绝域的临界值  。
。
根据图7-5给出的方差分析结果可知:
原料因素 =4.4174>
=4.4174>  =3.4903,拒绝原假设
=3.4903,拒绝原假设 
温度因素 =9.3939>
=9.3939>  =3.8853,拒绝原假设
=3.8853,拒绝原假设 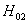
两因素的交互作用 =14.9288>
=14.9288> 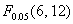 =2.9961,拒绝原假设
=2.9961,拒绝原假设 
因此,可以得出这样的结论:在显著性水平0.05下,原料和处理温度这两个因素对产品强度的影响都是显著的,且 =14.9288远大于
=14.9288远大于  =2.9961,故两者的交互作用效应是高度显著的。再比较图7-6中的求和或平均项可以看出,
=2.9961,故两者的交互作用效应是高度显著的。再比较图7-6中的求和或平均项可以看出,  与
与  或
或  与
与 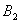 的搭配都使得产品强度较之其他水平的搭配要高得多。所以在实际中可以选最优的搭配方案
的搭配都使得产品强度较之其他水平的搭配要高得多。所以在实际中可以选最优的搭配方案  与
与  或
或 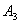 与
与  来生产这种金属材料。
来生产这种金属材料。
再如,某林场对果树采用了不同的剪枝方案和施肥方案进行试验(如图7-7所示),观察剪枝和施肥对果树的产量是否有显著影响?两者的交互作用是否显著?
在这里,试验的指标是果树产量,剪枝和施肥是因素,它们分别有3个、4个水平,这也是一个双因素的试验。试验的目的是要考察在各种因素的各个水平下果树产量有无显著的差异。即既要考虑不同的剪枝方案、不同的施肥方案是否对果树产量有显著影响,还要考虑剪枝和施肥两因素各方案的配合对果树产量是否有影响作用。

图7-6

图7-7 利用Excel 2000提供的方差分析:可重复双因素分析工具,取显著性水平 =0.05,得方差分析结果如图7-8所示。
=0.05,得方差分析结果如图7-8所示。
分析图7-8中的结果可知:
剪枝因素 =15.00942>
=15.00942>  =3.40283,拒绝原假设
=3.40283,拒绝原假设 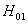
施肥因素 =5.55583>
=5.55583> 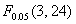 =3.00879,拒绝原假设
=3.00879,拒绝原假设 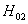
两因素的交互作用 =1.48807<
=1.48807< 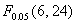 =2.50819,接受原假设
=2.50819,接受原假设 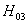

图7-8
因此,可以得出这样的结论:在显著性水平0.05下,剪枝和施肥都对果树产量有显著的影响,但两者的配合对果树产量无显著作用,即剪枝和施肥间无交互作用。
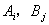 )至少要做2次试验,否则就不能将交互作用与误差分离开来。但如果在处理实际问题时,已经知道不存在交互作用,或已知交互作用对试验的指标影响很小,则可以不考虑交互作用。此时,即使k=1,也能对因素A、因素B的效应进行分析。因此对于两个因素的每一组合(
)至少要做2次试验,否则就不能将交互作用与误差分离开来。但如果在处理实际问题时,已经知道不存在交互作用,或已知交互作用对试验的指标影响很小,则可以不考虑交互作用。此时,即使k=1,也能对因素A、因素B的效应进行分析。因此对于两个因素的每一组合( 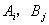 )只做一次试验即可,故称为双因素无重复试验,相应的方差分析称为双因素无重复试验的方差分析。
)只做一次试验即可,故称为双因素无重复试验,相应的方差分析称为双因素无重复试验的方差分析。
对于上节观察剪枝和施肥对果树的产量是否有显著影响的例子,通过分析结果知:剪枝和施肥这两个因素的配合对果树产量无显著作用,也就是说剪枝和施肥间无交互作用。对此就可以不考虑交互作用,对于两个因素的每一组合( )只做一次试验,即进行双因素无重复试验就可以了。
)只做一次试验,即进行双因素无重复试验就可以了。
现假设两个因素的无重复试验结果如下表所示。
再设 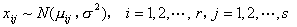 ,各
,各 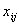 相互独立,其中
相互独立,其中  均为未知参数。则双因素无重复试验的方差分析只需要检验以下两个假设:
均为未知参数。则双因素无重复试验的方差分析只需要检验以下两个假设:
行因素A的检验(即检验因素A的每个水平 的效应
的效应  是否都等于零)
是否都等于零)
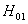 :
: 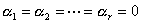
 :至少有一个
:至少有一个  不为零
不为零
列因素B的检验(即检验因素B的每个水平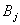 的效应
的效应  是否都等于零)
是否都等于零)
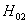 :
: 
 :至少有一个
:至少有一个  不为零
不为零
通过与双因素重复试验的方差分析中的同样讨论,可得双因素无重复试验的方差分析表,如下表所示。
取显著性水平为  ,可得假设
,可得假设 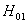 :
: 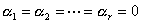 的拒绝域为
的拒绝域为

假设 :
: 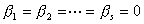 的拒绝域为
的拒绝域为
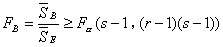
通过本章内容的学习,应掌握Excel 2000的单因素方差分析和双因素重复试验方差分析工具,并能熟练地运用于实际工作中。
下面利用Excel 2000提供的方差分析:可重复双因素分析工具求解本例。具体操作步骤如下:
选择工具菜单中的数据分析命令,此时弹出数据分析对话框。
在分析工具列表框中,选方差分析:可重复双因素分析工具。
这时弹出方差分析:可重复的双因素分析对话框,如图7-4所示。

图7-4
在输入框中指定输入参数。在输入区域框中指定试验数据所在区域A1:D9(通常为了使输出结果容易阅读理解,在原始数据区域中应包含标识行和列的标记信息);在每一样本的行数中键入2(因本例的每种原料有两行数据,即对因素A、B的水平的每对组合进行了t=2次试验);在
在输出选项框内指定输出选项。本例选定输出区域,并键入输出区域左上角单元格地址A11。
单击确定按钮。
所得本例的方差分析结果如图7-5所示。

图7-5
在图7-5给出的统计结果中,单元格区域A46:E52中的数据正好与表7-2所示的双因素重复试验方差分析表中的各个统计量相对应,其中样本即为行因素A,列即为列因素B,交互即为因素A与B的交互作用,内部即为误差,总计即为总和,差异源即为方差来源,SS即为平方和,df即为自由度,MS即为均方,F即为F比,P-value为接受原假设
根据图7-5给出的方差分析结果可知:
原料因素
温度因素
两因素的交互作用
因此,可以得出这样的结论:在显著性水平0.05下,原料和处理温度这两个因素对产品强度的影响都是显著的,且
再如,某林场对果树采用了不同的剪枝方案和施肥方案进行试验(如图7-7所示),观察剪枝和施肥对果树的产量是否有显著影响?两者的交互作用是否显著?
在这里,试验的指标是果树产量,剪枝和施肥是因素,它们分别有3个、4个水平,这也是一个双因素的试验。试验的目的是要考察在各种因素的各个水平下果树产量有无显著的差异。即既要考虑不同的剪枝方案、不同的施肥方案是否对果树产量有显著影响,还要考虑剪枝和施肥两因素各方案的配合对果树产量是否有影响作用。

图7-6

图7-7 利用Excel 2000提供的方差分析:可重复双因素分析工具,取显著性水平
分析图7-8中的结果可知:
剪枝因素
施肥因素
两因素的交互作用

图7-8
因此,可以得出这样的结论:在显著性水平0.05下,剪枝和施肥都对果树产量有显著的影响,但两者的配合对果树产量无显著作用,即剪枝和施肥间无交互作用。
7.2.2 无重复试验的方差分析
在上节的讨论中,考虑了双因素试验中两个因素的交互作用。为要检验交互作用的效应是否显著,对于两个因素的每一组合(对于上节观察剪枝和施肥对果树的产量是否有显著影响的例子,通过分析结果知:剪枝和施肥这两个因素的配合对果树产量无显著作用,也就是说剪枝和施肥间无交互作用。对此就可以不考虑交互作用,对于两个因素的每一组合(
现假设两个因素的无重复试验结果如下表所示。
| 因素B 因素A | B1 | B2 | … | Bs |
| A1 | x11 | x12 | … | x1s |
| A2 | x21 | x22 | … | x2s |
| … | … | … | … | … |
| Ar | xr1 | xr2 | … | xrs |
行因素A的检验(即检验因素A的每个水平
列因素B的检验(即检验因素B的每个水平
通过与双因素重复试验的方差分析中的同样讨论,可得双因素无重复试验的方差分析表,如下表所示。
| 方差来源 | 平方和 | 自由度 | 均方 | F 比 |
| 因素A | ||||
| 因素B | ||||
| 误差 | ||||
| 总和 |
假设
通过本章内容的学习,应掌握Excel 2000的单因素方差分析和双因素重复试验方差分析工具,并能熟练地运用于实际工作中。
(责任编辑:admin)
顶一下
(0)
0%
踩一下
(0)
0%
最新内容
推荐内容




